इस आर्टिकल में हम "Boolean Algebra" को पढ़ने और समझने वाले है। इसमें हम "Boolean Algebra क्या होता है, Boolean Functions, Logic Diagram, इसके Laws और Rules, DeMorgan Theorem. आर्टिकल में Boolean Algebra को अच्छी तरह कवर करेंगे जिससे आपके concepts क्लियर हो सके।
Table of Contents
Boolean Algebra क्या होता है?
Boolean Algebra एक गणितीय सरंचना है जिसमे कुछ operations निर्धारित किये गए है। इन Operations को Binary Variables(चर) पर perform किया जाता है।
इस क्रिया में दो values 1 या 0 ही हो सकती है। 1 और 0 को हम True और False, सत्य और असत्य या On और Off से भी व्यक्त कर सकते है।
Boolean Algebra का अविष्कार, George Boole द्वारा किया गया था। उन्होंने 1847 में लिखी अपनी किताब "The Mathematical Analysis of Logic" में इसके बारे में बताया था।
Boolean Algebra में मुख्यतः 3 Logical Operations किये जाते है, AND, OR, और NOT. इन्ही operations की मदद से logical values और Expressions को manipulate किया जाता है।
जैसे AND operation में 1 तभी प्राप्त होता है जब दोनों Operands (इनपुट) 1 हो। इसी तरह OR operation में 1 या True तभी प्राप्त होता है जब कम से कम एक operand 1(True) हो, इसी प्रकार NOT operation इनपुट value के विपरीत output प्रदान करता है।
 |
| Boolean Algebra In Hindi |
Boolean Values: True and False
Boolean Values किसी statement या condition के सत्य या असत्य होने को दर्शाता है। चलिए इसे अच्छी तरह समझते है। उदाहरण के लिए "आसमान का रंग नीला है" यह statement सत्य और असत्य हो सकता है, यह इस बात पर निर्भर करेगा की फ़िलहाल दिन है या रात, या यूँ कहे की फ़िलहाल आसमान का रंग कैसा है।
बूलियन अलजेब्रा में सत्य और असत्य को 1 और 0 से दर्शाया जाता है। 1 और 0 को आप "Yes" और "No" या "On" और "Off" तथा "High" और "Low" भी कह सकते है। कहने का अर्थ है जहा जिस फील्ड में आप boolean algebra का प्रयोग कर रहे है आप 1 और 0 को उसी नाम से बोल सकते है।
Also Read: Logic Gates In Hindi
Boolean Operators: AND, OR, and NOT
बूलियन ऑपरेटर्स का प्रयोग, बूलियन वैल्यूज या expressions को manipulate( एक प्रकार से जोड़, गुणा, भाग) करने के लिए किया जाता है। इसके लिए 3 प्रमुख बूलियन ऑपरेटर्स है। AND, OR,एवं NOT Operator. चलिए इनके बारे में थोड़ा जान लेते है।
AND Operator
AND Operator में हमें 1 (सत्य) value तभी प्राप्त होती है जब दोनों इनपुट/Operands values 1/सत्य होती है। अन्यथा हमे 0 (असत्य) value प्राप्त होती है। इसे "AND" से या "∧" symbol से दर्शाया जाता है। उदाहरण के लिए मान लीजिये A इनपुट की वैल्यू है "आज आसमान साफ़ है" तथा B इनपुट की वैल्यू है "आज वर्षा नहीं होगी" तो A AND B expression की वैल्यू True/1/सत्य तभी होगी जब A और B की वैल्यू 1/True/सत्य होगी।
OR Operator
AND Operator में हमें 1 (सत्य) value तभी प्राप्त होती है जब कम से कम एक "इनपुट/Operands values" 1(सत्य) होती है। जब दोनों इनपुट values 0 होती है तब हमे आउटपुट में 0 value प्राप्त होती है। इसे "OR" या "∨" Symbol द्वारा represent किया जाता है। चलिए पिछले उदाहरण से ही OR ऑपरेटर का कार्य समझते है। A OR B की Value True होगी अगर A या B में कम से कम किसी एक की या दोनों की value 1 होगी।
NOT Operator
NOT Operator इनपुट वैल्यू के विपरीत रिजल्ट देता है। इसे "NOT" या "~" Symbol द्वारा दर्शाया जाता है। मान लीजिये A की value है "वर्षा हो रही है" तो NOT A की value सत्य तब होगी जब "वर्षा नहीं हो रही होगी"
Laws and Rules of Boolean Algebra
Boolean Algebra के कुछ नियम और Laws है जिनकी सहयता से Boolean Expressions को simplify किया जाता है। इन्ही नियमों की सहयता से जटिल expressions को एक systematic तरीके से simplify किया जाता है। इसलिए इन नियमों को समझना अत्यंत जरुरी है। Boolean algebra के कुछ महत्वपूर्ण laws और rules इस प्रकार है-
Also Read: De Morgan Theorem In Hindi
Associative Laws
Boolean Algebra के Associative Laws हमे यह बताते है की input/Operands को combine या grouping करने पर उनके output में कोई प्रभाव नहीं पड़ता है। Boolean Algebra में दो associative laws है:
1.Associative Law for OR
OR के लिए Associative Law हमे बताता है की OR operation की grouping को बदलने से आउटपुट पर कोई भी प्रभाव नहीं पड़ता है। उदाहरण के लिए
(A OR B) OR C का आउटपुट A OR (B OR C) के समान होगा।
2. Associative Law for AND
AND के लिए Associative Law हमे बताता है की AND Operation की Grouping को बदलने आउटपुट पर कोई भी प्रभाव नहीं पड़ता है। उदाहरण के लिए
(A AND B) AND C का आउटपुट A AND (B AND C) के समान होगा।
Distributive Laws
Distributive Laws हमे बताता है की Boolean variables और expressions के मध्य operations को किस प्रकार डिस्ट्रीब्यूट किया जा सकता है।
जैसे expression A OR (B AND C) को (A OR B) AND (A OR C) लिखा जाता है। इसे "OR over AND"कहा जाता है।
इसकी प्रकार expression A OR (B AND C) को (A OR B) AND (A OR C) इस तरह distribute किया जाता है, इसे "AND over OR" कहेंगे।
Commutative Laws
Boolean Algebra में Commutative Law हमें बताता है की इनपुट values के क्रम को बदलने से आउटपुट में कोई बदलाव नहीं होता है। इसको अच्छी तरह से समझने के लिए दो commutative laws है, OR तथा AND
OR Operation के लिए Commutative Law हमें बताता है की OR operation के क्रम को बदला जा सकता है तथा इससे आउटपुट पर कोई प्रभाव नहीं पड़ता है।
उदाहरण के लिए: A OR B = B OR A
AND Operation के लिए Commutative Law हमें बताता है की AND operation के क्रम को बदला जा सकता है तथा इससे आउटपुट पर कोई प्रभाव नहीं पड़ता है।
उदाहरण के लिए: A AND B = B AND A
De Morgan's Law
De Morgan Law हमे बताता है की negation(NOT) operation दूसरे लॉजिकल operations जैसे AND तथा OR के साथ कैसे interact करता है। इसमें दो laws है
First Law: Complement of a Conjunction
De Morgan का प्रथम law हमे बताता है की कोई दो variable जो AND operation में है उनका complement बराबर होगा उन दोनों के complement पर OR operation के। चलिए इसे एक equation से समझते है।
(A AND B)' = A' OR B'
इसका मतलब जब दोनों variable A तथा B False होंगे तब उनके conjunction(AND) का negation (NOT), True होगा। इसे निचे दिए गए Truth Table से Verify किया जा सकता है।
 |
| De Morgan First Law |
Second Law: Complement of a Disjunction
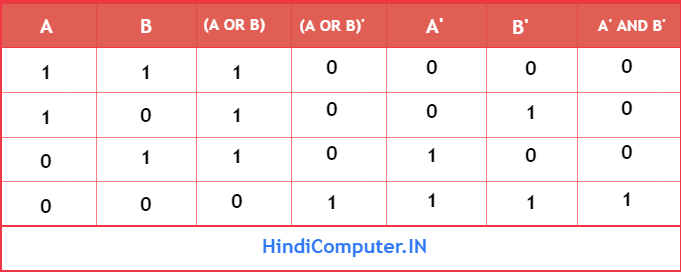
De Morgan का दूसरा Law हमे बताता है की दो वेरिएबल A तथा B पर OR operation किया जाए तथा उसके result का Complement(NOT) बराबर होगा NOT A और NOT B पर AND operation के। चलिए इसे एक equation से समझते है।
(A OR B)' = A' AND B'
इसका मतलब अगर A तथा B में अगर कोई भी variable True नहीं है तो (A OR B)' का result True होगा। इसे निचे दी गयी Truth Table से Verify किया जा सकता है।
 |
| De Morgan Second Law |
AND laws in Boolean algebra
- A AND 0 = 0
- A AND 1 = A
- A AND A = A
- A AND A' = 0
यहाँ
- A एक boolean variable को दर्शाता है
- 0 एक logical value है जिसका अर्थ False होता है
- 1 एक logical Value है जिसका अर्थ True होता है
- A' complement है A का, अर्थात NOT A
OR laws in Boolean algebra
- A OR 1 = 1
- A OR 0 = A
- A OR A = A
- A OR A' = 1
मुझे लगता है Exam के नजरिये से हमने Boolean Algebra पढ़ लिए है, आशा है इस आर्टिकल को पढ़ने के बाद आपको बूलियन अलजेब्रा समझने में आसानी होगी। अगर इसमें आप Boolean Properties या Question चाहते है तो आप Comment Box में हमे बता सकते है, हम इस article को update कर देंगे।




